Jリーグの入場者数を「中央値」を使ってまとめる

平均値の課題

入場者数を年度別やJ1～J3に分類し、平均入場者を見ることで傾向を知ることが出来ることが分かりました。

例えば、「平均」を使用して、J1の入場者数の傾向を説明することが現出来ます。
平均値については、こちらの記事にまとめています。

データの特徴を表現できる「平均」のことを統計の世界では「代表値」と言います。

イメージを共有する時に「平均」はとっても便利です。

しかし、データの内容によっては、特徴が正しく表現されないこともあります。

平均値の問題例

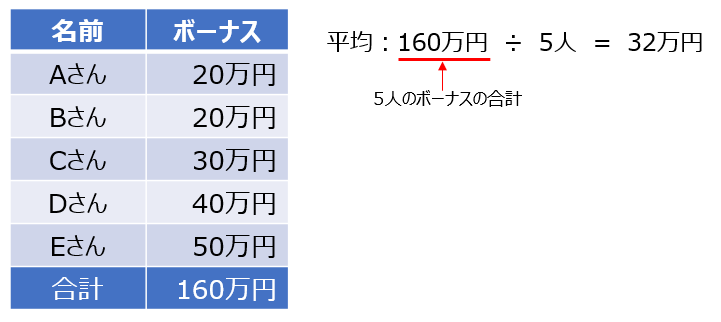
5人のサラリーマンがいてボーナスが支給されたとします。

平均は全員の合計を人数で割りますから、5人の平均は32万円で、どの人にとっても「そのぐらいなのかな？」と思えます。

客観的に見ても5人の状況を説明で平均32万円は、納得できると思います。

ちょっと極端ですが、Eさんのボーナスが50万円から1000万円にアップします。

この場合の平均は、一気に上がって222万円になります。

Aさん～Dさんは、「え？みんな、そんなにもらっているの？」という感想を持つと思います。

逆にＥさんも「平均より自分はだいぶ高いなぁ」と感じます。

平均値が5人の特徴を表しているとは、なかなか言えないでしょう。

平均はデータの中に極端に大きい・小さい数字が入り込むと実際の状況とは乖離が発生てしまいます。

そこで登場するのが、2つ目にご紹介する代表値、「中央値」です。

中央値の利用

中央値の算出に、計算はありません。
データを低い方から順番に並べて、ちょうど真ん中となる数字を数えます。

順番で真ん中となる数字のことを「中央値」と言います。

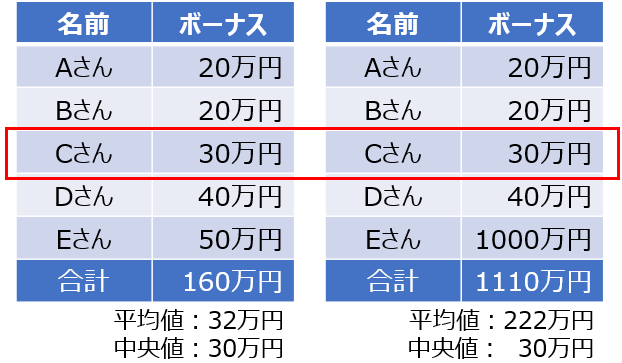
Ｅさんのボーナスが50万円・1000万円のどちらの場合だったとしても、真ん中はＣさんとなります。

Ｅさんのボーナスに関係なく中央値は30万円になります。

このように中央値は、極端な数字に引っ張られることなく、そのデータを説明することが出来ます。

Ｅさんのボーナスが50万円の場合には、代表値として「平均値の32万円」「中央値の30万円」どちらを利用しても問題ありません。

しかし、Ｅさんのボーナスが1000万円の場合は、「中央値の30万円」を利用した方が適切な場面が多そうです。

「平均」は便利なので、いろんな場面で利用されます。

しかし、本当にその数字が対象データを表現できているのかは注意が必要になります。

Jリーグの入場者数の平均値と中央値

前置きが長くなってしまいましたが、Ｊリーグの「中央値」を見ていきます。

各年度の平均値と中央値をグラフに表しました。

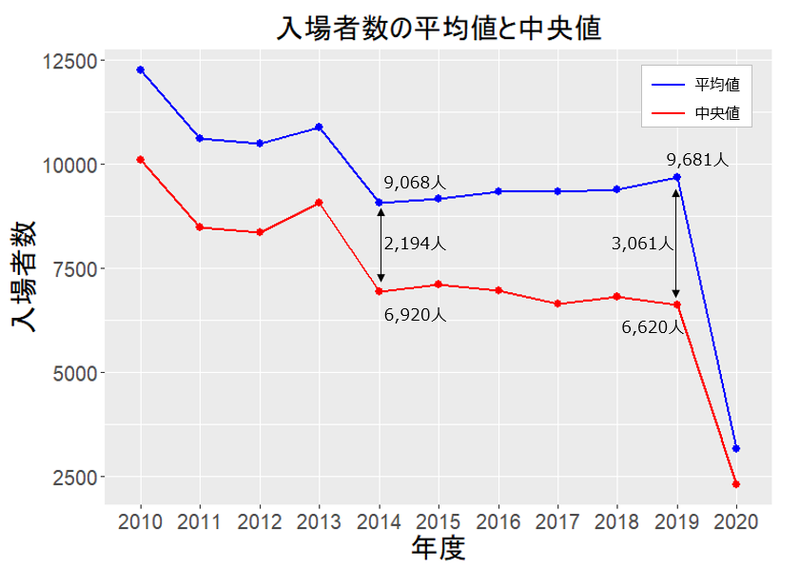
ほぼ、連動した動きをしていることが分かります。

ただし、「中央値」が「平均値」より大きくなることはありません。

また、少しだけ平均値は中央値より増加傾向と言えるかもしれません。

中央値は、2014年と2019年の差は300人なので、ほとんど変わっていません。

平均値と中央値の違いのまとめ

平均値と同じですが、カテゴリによって特徴が異なることが想定されるので、次回は、中央値をJ1～J3に分解して分析していきます。